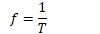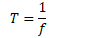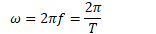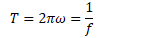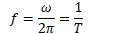Simple Harmonic Motion

  • Simple harmonic motion (SHM) is motion in which a restoring force is directly proportional to the displacement of an object

  • Nature's response to a perturbation or disturbance is often SHM

Circular Motion vs. SHM

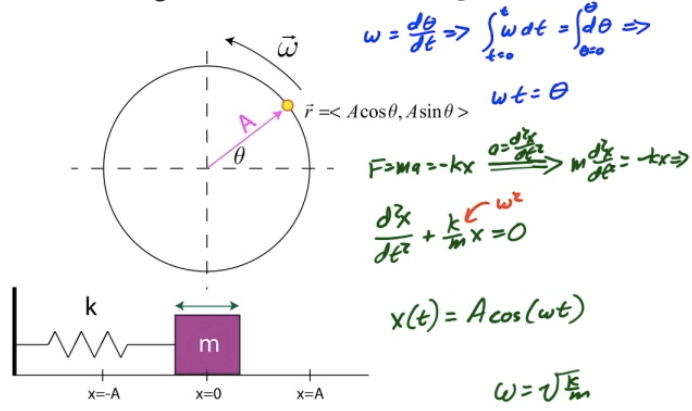
ř AcosO,AsinO > A Cos W; tJk.

Position, Velocity, Acceleration

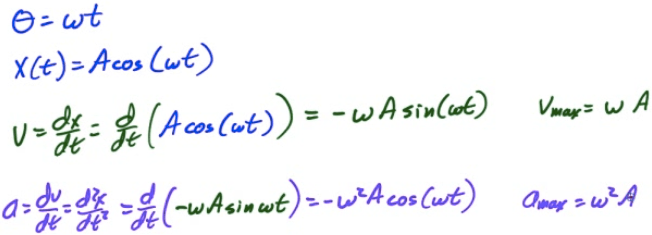
C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image275.png

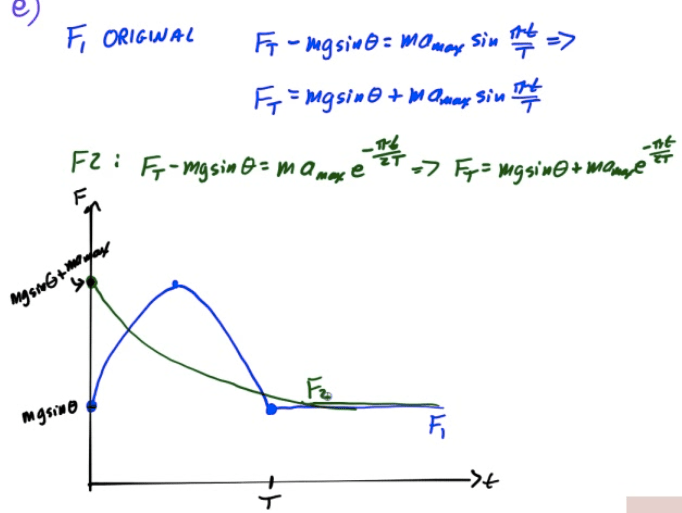
Frequency and Period

  • Frequency

    • Frequency is the number of revolutions or cycles which occur each second

    • Symbol is f

    • Units are 1/s, or Hertz (Hz)

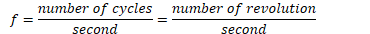
    • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image276.png

  • Period

    • Period is the time it takes for one complete revolution, or cycle.

    • Symbol is T

    • Unites are seconds (s)

    • T = time for 1 cycle = time for 1 revolution

  • Relationship

    • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image167.png

    • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image168.png

Angular Frequency

  • Angular frequency is the number of radians per second, and it corresponds to the angular velocity for an object traveling in uniform circular motion

  • Relationship

    • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image277.png

    • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image278.png

    • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image279.png

Example 1: Oscillating System

  • An oscillating system is created by a releasing an object from a maximum displacement of 0.2 meters. The object makes 60 complete oscillations in one minute

  • Determine the object's angular frequency

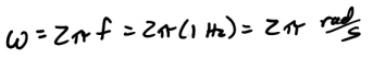
    C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image280.png

  • What is the object's position at time t=10s?

    C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image281.png

  • At what time is the object at x=0.1m?

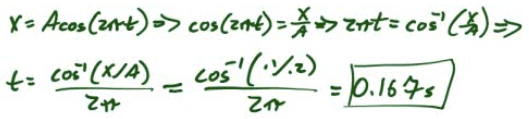
    C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image282.png

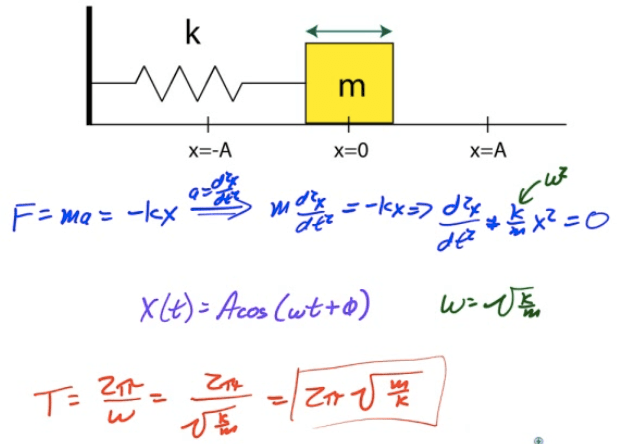
Mass on a Spring

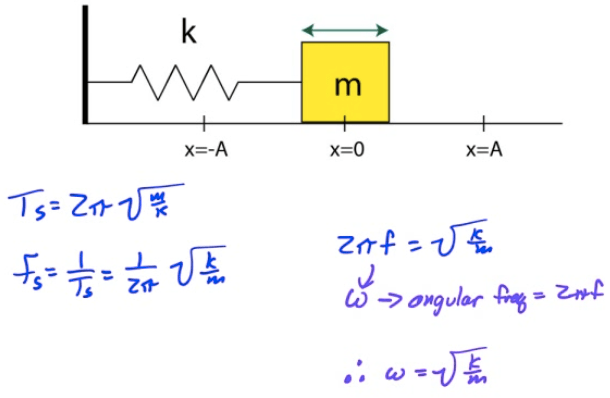
k zrrC

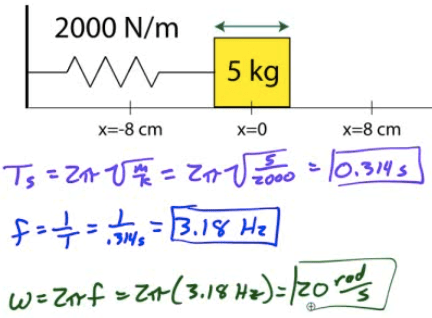
Example 2: Analysis of Spring-Block System

  • A 5-kg block is attached to a 2000 N/m spring as shown and displaced a distance of 8 cm from its equilibrium position before being released.

  • Determine the period of oscillation, the frequency, and the angular frequency for the block

    2000 N/m 5 kg x=-8 cm cm Ts

General Form of SHM

dt2

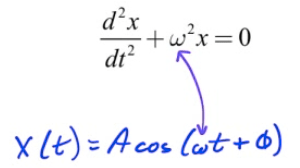
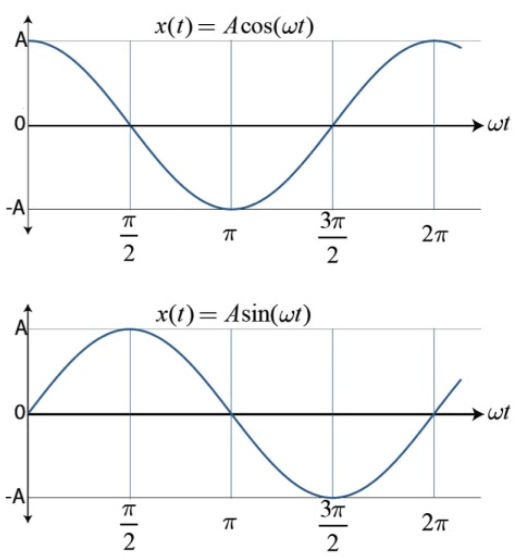
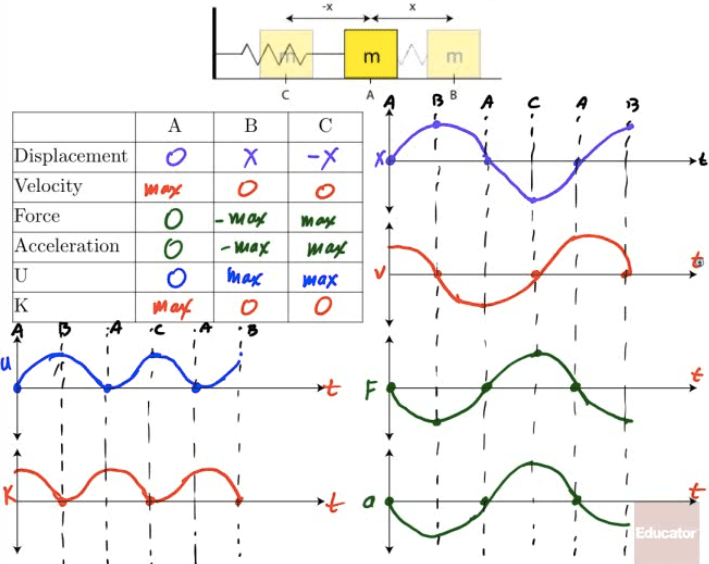
Graphing SHM

x(t) = A cos(wt) x(t) Asin(wt) 27

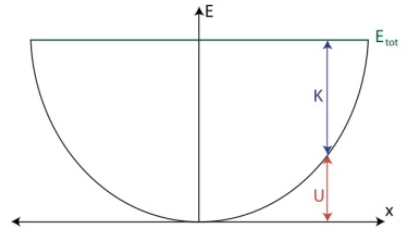
Energy of SHM

  • When an object undergoes SHM, kinetic and potential energy both vary with time, although total energy (E=K+U) remains constant

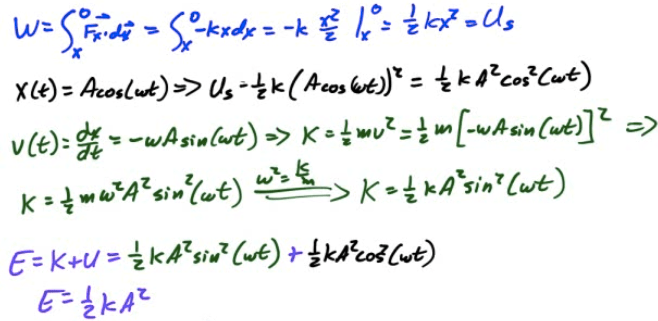
    C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image287.png

Horizontal Spring Oscillator

m X de) Atos (u,++O)

Vertical Spring Oscillator

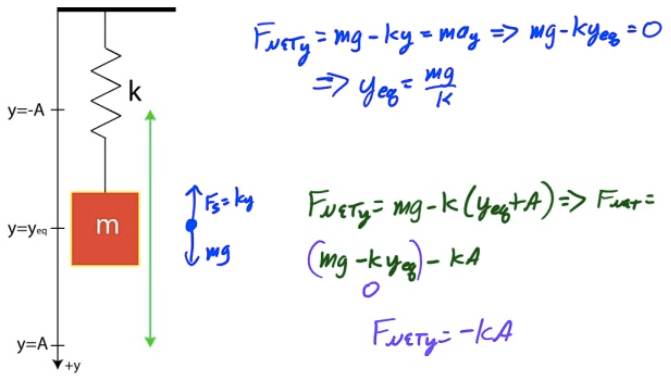
k y=yeq

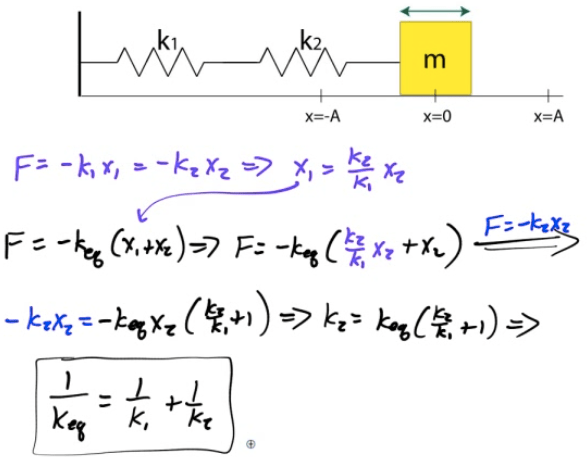
Springs in Series

kl

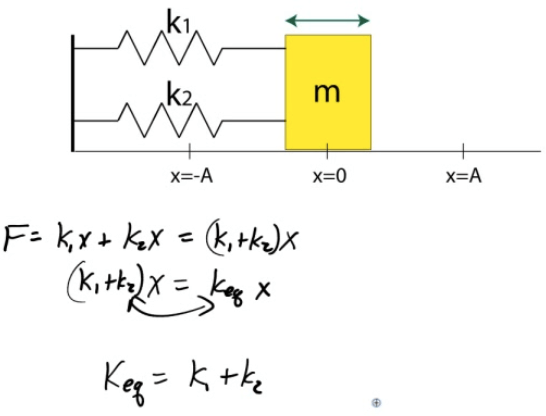
Springs in Parallel

kl k2 x=-A m x=A

The Pendulum

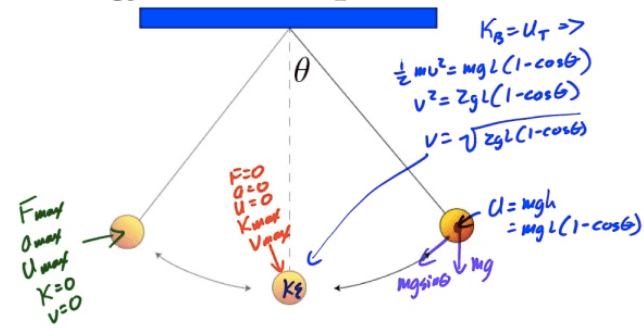
  • A mass m is attached to a light string that swings without friction about the vertical equilibrium position

    θ

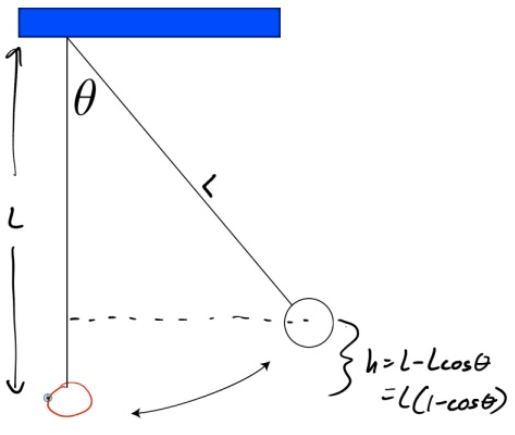
Energy and the Simple Pendulum

ومهى. -(1- -دمه 162 an -مههم دا/ z— n «٥ي م7(1-

C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image294.png

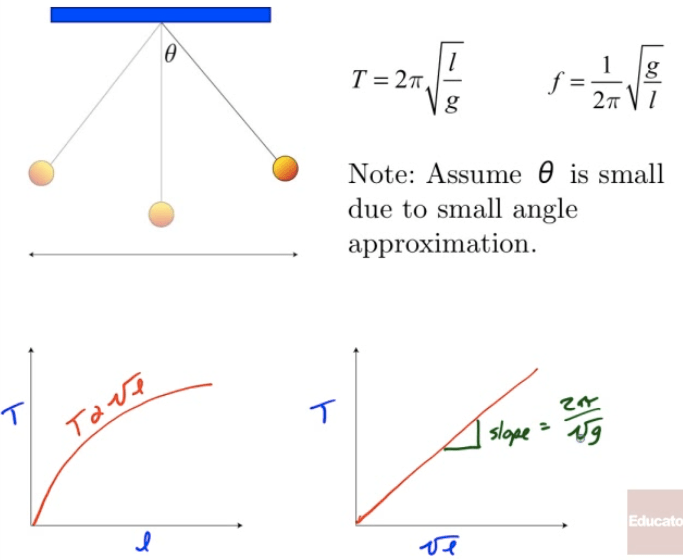
Frequency and Period of a Pendulum

27r I Note: Assume 9 is small due to small angle approximation. 43

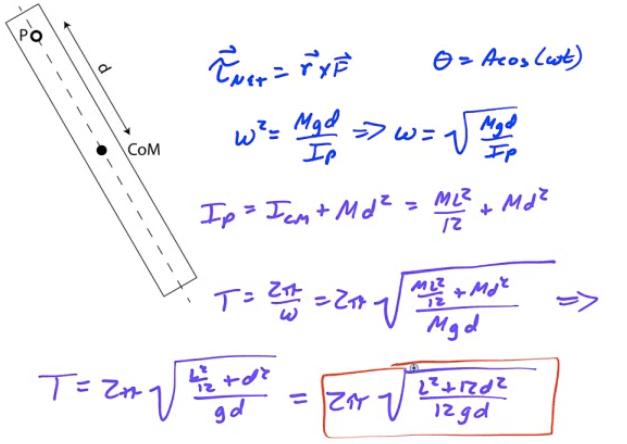
Period of a Physical Pendulum

The Physical Pendulum A physical pendulum is an oscillating body that rotates according to the location of its center of mass rather than a simple pendulum where all the mass is located at the end of a light string. mu sin B mg It is important to understand that "d" is the lever arm distance or the distance from the COM position to the point of rotation. It is also the same "d" in the Parallel Axes theorem. Frsin9 = = la —mg sin Q/ = Ia, d = — mgd = la sine = 9 mgd)9 = o mgd p pen du/ mgd

Example 3: Deriving Period of a Simple Pendulum

C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image297.png

Example 4: Deriving Period of a Physical Pendulum

492 2PW+ -C

Example 5: Summary of Spring-Block System

orce elocity cceleration isplacement ㄨ 0

Example 6: Harmonic Oscillator Analysis

  • A 2-kg block is attacked to a spring. A force of 20 N stretches the spring to a displacement of 0.5 meter

  • The spring constant

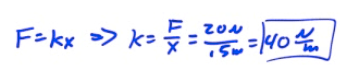
    C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image300.png

  • The total energy

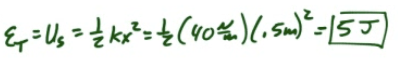
    工 5 , , ・ ノ ( 。 り ト 物 ト 勿 = つ

  • The speed at the equilibrium position

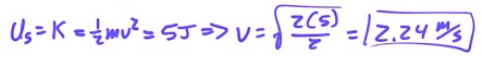
    C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image302.png

  • The speed at x=0.30 meters

    2 24-9 z

  • The speed at x=-0.4 meters

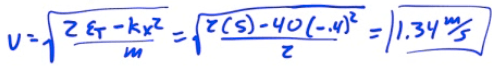
    C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image304.png

  • The acceleration at the equilibrium position

    C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image305.png

  • The magnitude of the acceleration at x=0.5 meters.

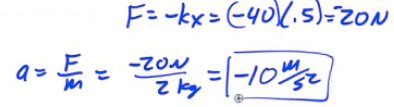
    F: s)v-zoa.'

  • The net force at equilibrium position

    C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image307.png

  • The net force at x=0.25 meter

    e -100

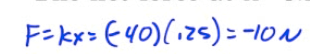
  • Where does kinetic energy = potential energy

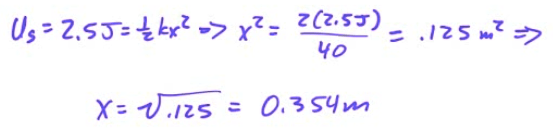
    'Mt'S €0 -X Oh

Example 7: Vertical Spring Block Oscillator

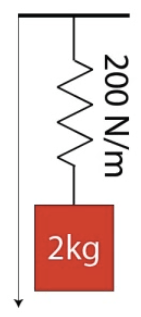
200 N/m

  • A 2-kg block attached to an un-stretched spring of spring constant k=200 N/m as shown in the diagram below is released from rest. Determine the period of the block's oscillation and the maximum displacement of the block from its equilibrium while undergoing simple harmonic motion.

    -za.2

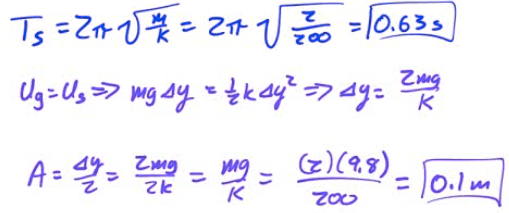
2009 Free Response Question 2

x Mech. 2. You are given a long, thin, rectangular bar of known mass M and length t with a pivot attached to one end. The bar has a nonuniform mass density, and the center of mass is located a known distance x from the end with the pivot. You are to determine the rotational inertia 1b of the bar about the pivot by suspending the bar from the pivot, as shown above, and allowing it to swing. Express all algebraic answers in terms of 1b , the given quantities, and fundamental constants. (a) i. By applying the appropriate equation of motion to the bar, write the differential equation for the angle 9 the bar makes with the vertical. ii. By applying the small-angle approximation to your differential equation, calculate the period of the bar's motion. (b) Describe the experimental procedure you would use to make the additional measurements needed to determine 1b. Include how you would use your measurements to obtain 1b and how you would minimize experimental error. (c) Now suppose that you were not given the location of the center of mass of the bar. Describe an experimental procedure that you could use to determine it, including the equipment that you would need.

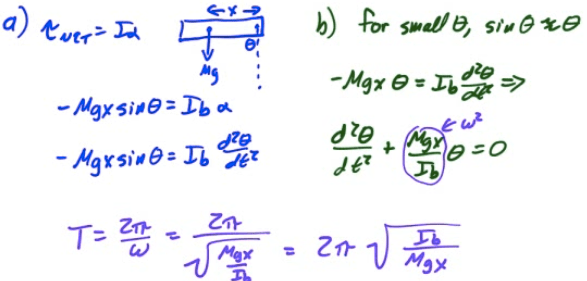
Z•rp ZQ

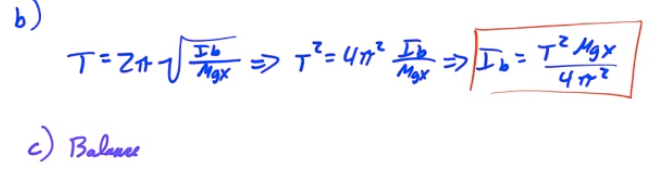
C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image314.png

2010 Free Response Question 3

Mech. 3. A skier of mass m will be pulled up a hill by a rope, as shown above. The magnitude of the acceleration of the skier as a function of time t can be modeled by the equations a = a sin where amax and T are constants. The hill is inclined at an angle 9 above the horizontal, and friction between the skis and the snow is negligible. Express your answers in terms of given quantities and fundamental constants. (a) Derive an expression for the velocity of the skier as a function of time during the acceleration. Assume the skier starts from rest. (b) Derive an expression for the work done by the net force on the skier from rest until terminal speed is reached. (c) Determine the magnitude of the force exerted by the rope on the skier at terminal speed. (d) Derive an expression for the total impulse imparted to the skier during the acceleration. -rt/2T (e) Suppose that the magnitude of the acceleration is instead modeled as a = amaxe for all t > O , where amax and T are the same as in the original model. On the axes below, sketch the graphs of the force exerted by the rope on the skier for the two models, from t = O to a time t > T . Label the original model Fl and the new model F2 .

Za.„T

C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image317.png

C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image318.png

results matching ""

    No results matching ""