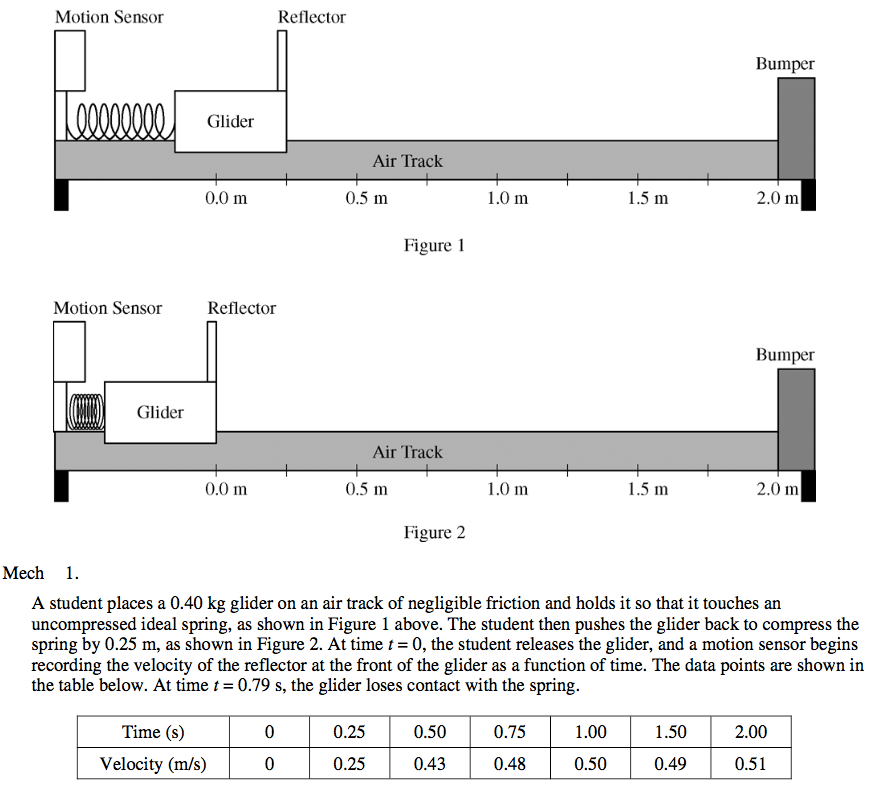
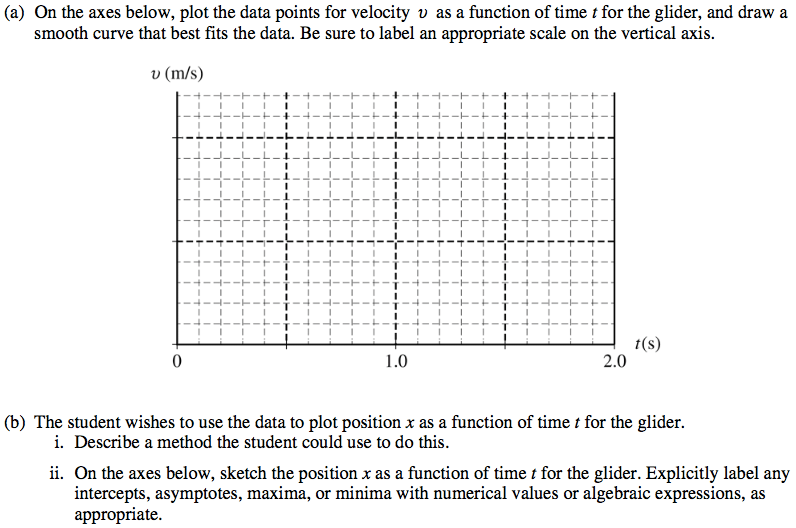
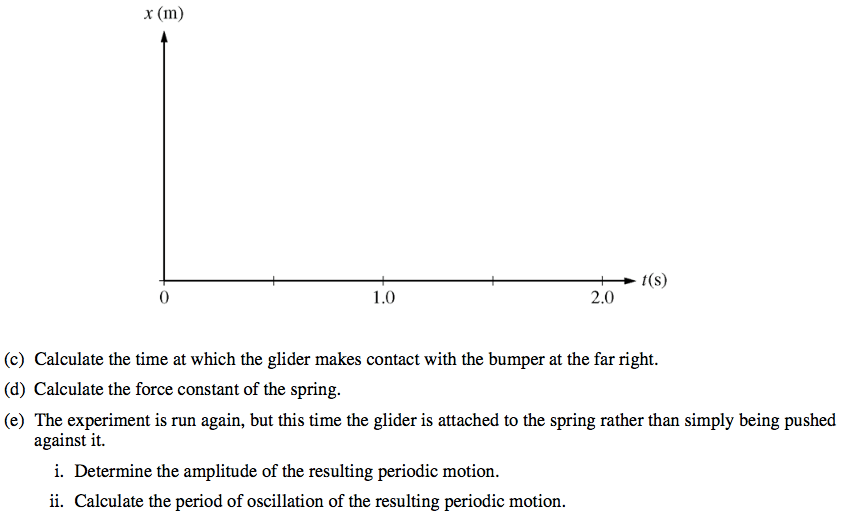
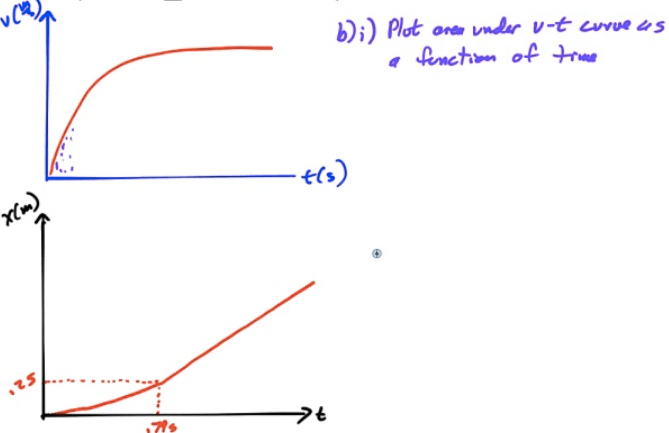
Conservation of Mechanical Energy
Consider a single conservative force doing work on a closed system
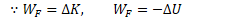
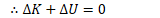
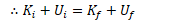
Non-Conservative Forces
Non-conservative forces change the total mechanical energy of a system, but not the total energy of a system
Work done by a non-conservative force is typically converted to internal (thermal) energy
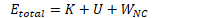
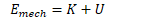
2002 Free Response Question 3
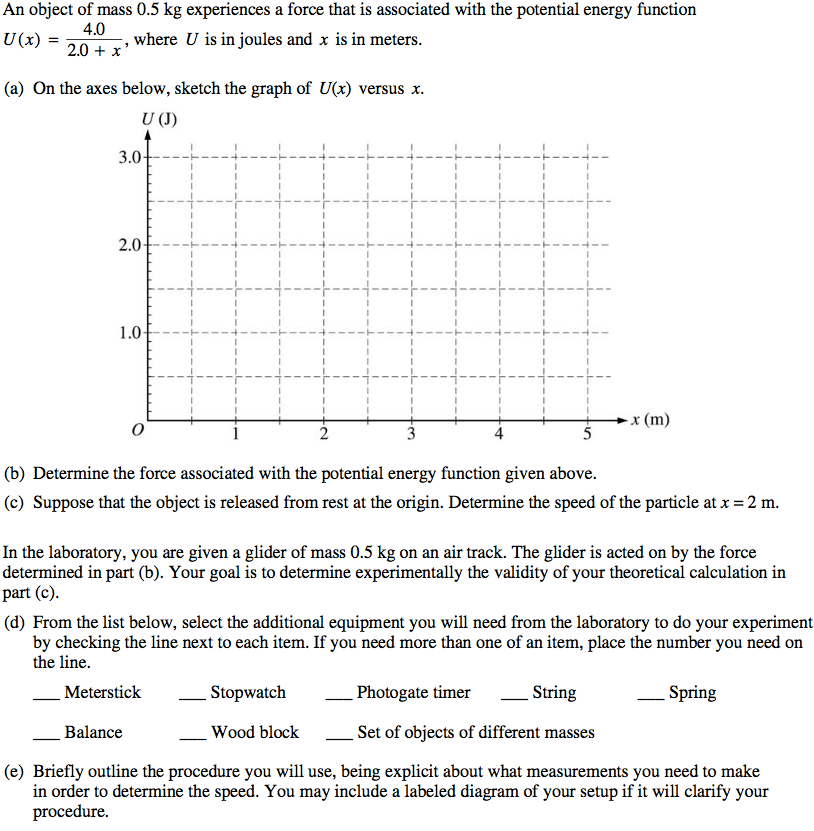
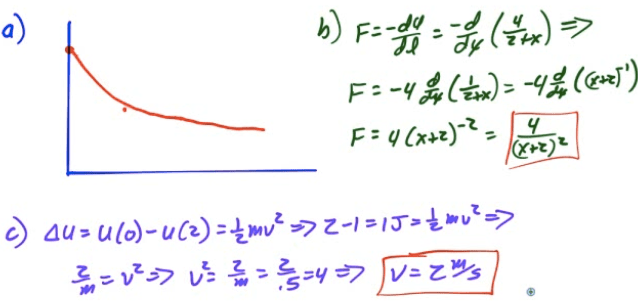

2007 Free Response Question 3
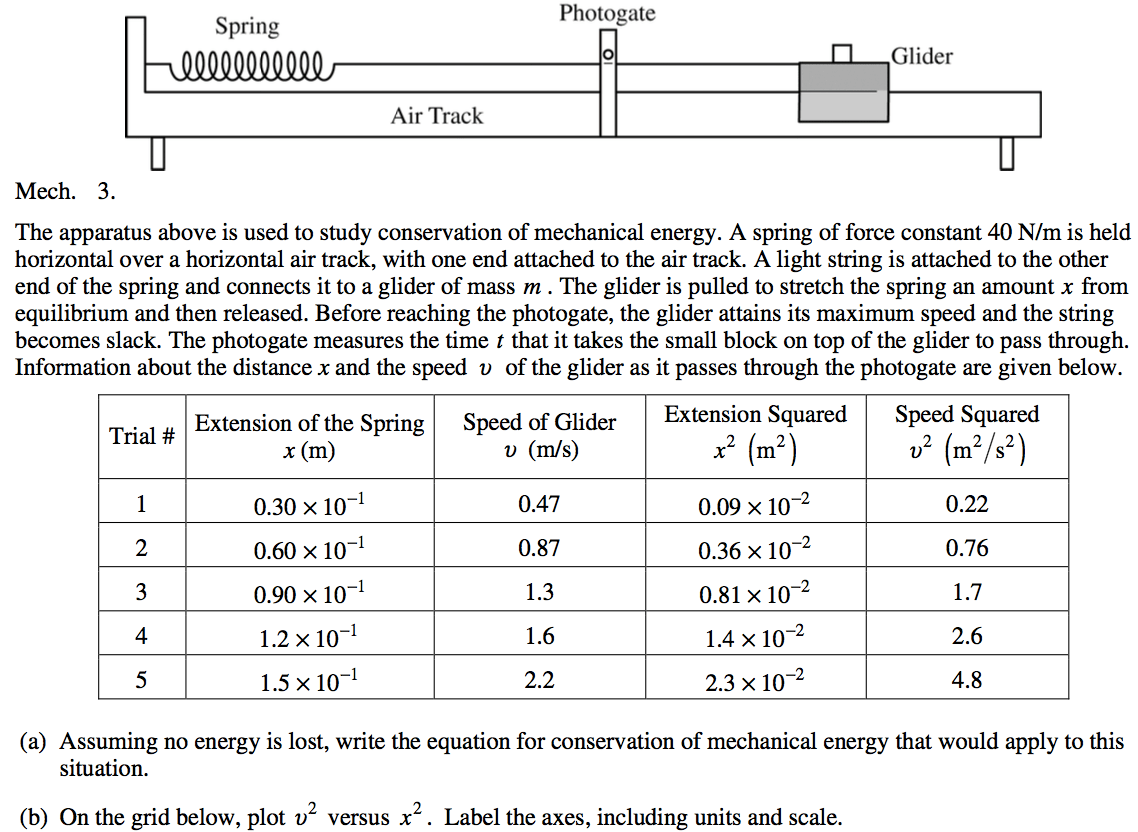
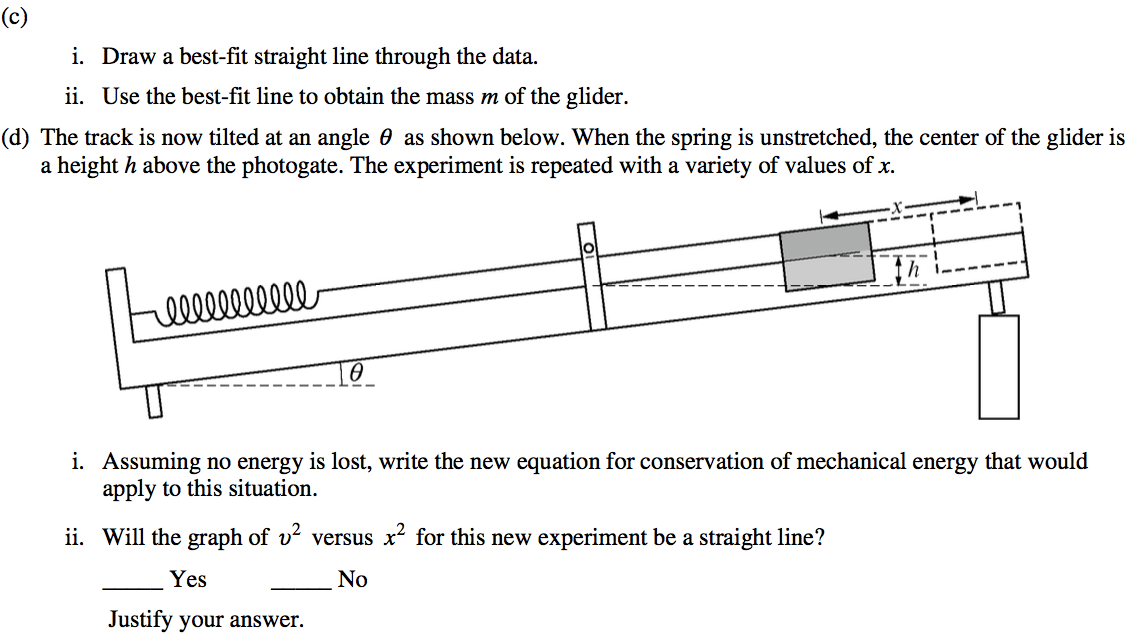
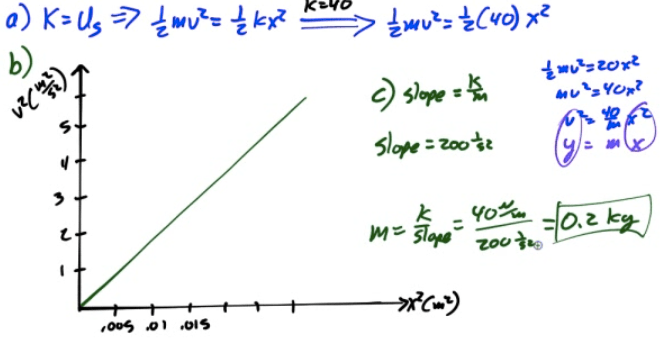
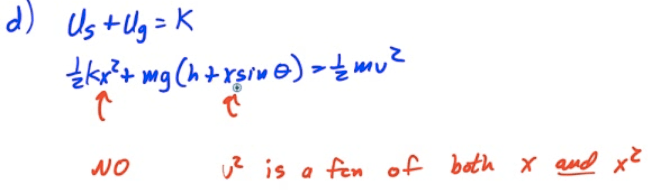
2010 Free Response Question 1



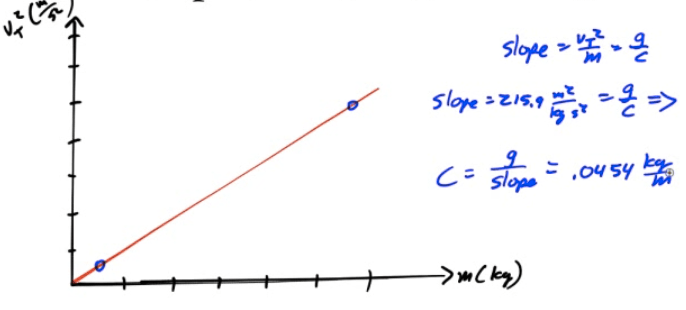
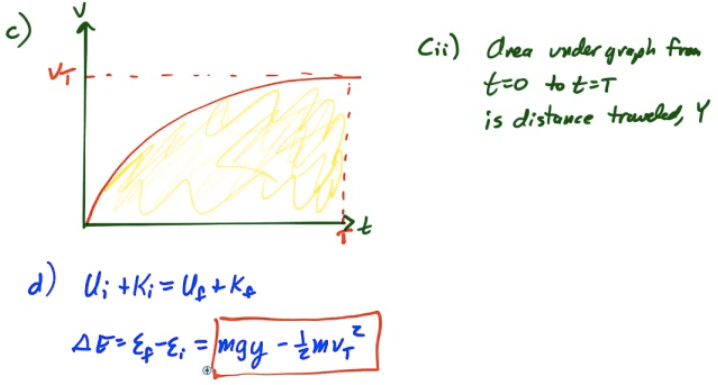
2013 Free Response Question 1